Partie II : Les accords

 Retour Projet

            Déf : Un accord en musique est un ensemble de notes qui sont jouées en même temps. L’accord le plus connu étant l’accord parfait qui sonne tout a fait bien à l’oreille.

                        1. Algorithme

 Voilà comment nous allons procéder pour mettre en place les notes des accords :

         -Dans la partie précédente, on a pris la partie entière de g. On en prend ici sa partie décimale : on a donc un nombre décimal à 2 décimales.

         -Dans un premier temps, on multiplie se nombre par 10 et on en prend la partie entière de façon à avoir un chiffre compris entre 0 et 9.

         - Ce chiffre va nous permettre de construire notre accord grâce aux intervalles. Un intervalle est une « distance » entre deux notes. On a une fois de plus décomposé les intervalles en demi-tons. C'est-à-dire que l’on associe à chaque intervalle le nombre de demi-tons qu’il vaut :

   Les intervalles que l’on utilise sont tous justes (Quarte,Quinte,Octave,Onzième) ou majeurs (tous les autres).

Donc le chiffre que l’on aura obtenu nous donnera le nombre de demi-tons à ajouter à la note fondamentale (première partie).

         - Pour le deuxième intervalle, on reprend la partie décimale du dessus, on la multiplie cette fois-ci par 100, et on obtient un chiffre compris, encore une fois, entre 0 et 9.

         - On refait alors de même que précédemment.

On a donc obtenu un accord suivant un nombre, et on refait cette manipulation autant de fois qu’il est nécessaire.

  Retour en haut de page 

               2. Loi de calcul

          On prend le principe des intervalles. C'est à dire que suivant les chiffres en troisième et quatrième position dans le groupe initial de quatre chiffres, on rajoute un intervalle à la note fondamentale pour avoir un accord de trois notes maximum.

         - Si le chiffre est 0, on ne rajoute pas d'intervalle.

         - Si le chiffre est 1, on rajoute une seconde majeure à la note fondamentale (2 demi-tons).

         - Si le chiffre est 2, on rajoute une tierce majeure à la note fondamentale (4 demi-tons).
         - Si le chiffre est 3, on rajoute une quarte juste à la note fondamentale (5 demi-tons).

         - Si le chiffre est 4, on rajoute une quinte juste à la note fondamentale (7 demi-tons).

         - Si le chiffre est 5, on rajoute une sixte majeure à la note fondamentale (9 demi-tons).

         - Si le chiffre est 6, on rajoute une septième majeure à la note fondamentale (11 demi-tons).

         - Si le chiffre est 7, on rajoute une octave juste à la note fondamentale (12 demi-tons).

         - Si le chiffre est 8, on rajoute une neuvième majeure (seconde majeure) à la note fondamentale (14 demi-tons).

         - Si le chiffre est 9, on rajoute une dixième majeure (tierce majeure) à la note fondamentale (16 demi-tons).

         Pour ajouter les intervalles dans le programme, on les transforme en demi-tons et on les ajoute au reste trouvé précédemment dans la division de c par douze (ce nombre été appelé n). L’addition de ces deux nombres nous donne le nombre m. On fait ensuite la division de ce nombre m par douze et on reprend la loi de calcul exposée dans la partie I pour lui associer une note suivant le reste obtenu On a donc des accords qui sont composés au maximum de trois notes.

         Pour le chiffre en quatrième position, on réitère l'opération.

                   3. Partie du programme correspondante

                  4. Elaboration de la partition

     Nous avons donc ici les 20 premiers accords de notre production . 

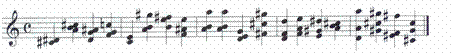
Pour écouter l'extrait sonore obtenu cliquez ici

Retour en haut de page