Le
nombre d'or était connu des anciens Grecs;
Euclide a résolu le problème de la section
dorée d'un segment de droite. Même aujourd'hui,
le nombre d'or reste un sujet d'intérêt pour
plusieurs. Mais qu'est-ce que le nombre d'or
?
Le " nombre d’or ",
ou " section dorée ",
ou " proportion dorée ",
est un nombre égal à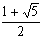 
, soit environ 1,618033988749....
Ce nombre correspondrait au partage le plus
harmonieux d’une grandeur en deux parties
inégales.
Si a et
b (a étant plus grand que b)
sont les deux parties de la grandeur
p,
On a :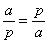 
Comme p = a +
b, on trouve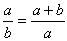 
, donc a2 = ab + b2.
En donnant la valeur 1 au plus petit,
c’est-à-dire à b, on trouve :
a2 - a = 1 , donc a2
-a -1 = 0.
La racine positive de cette équation du second
degré est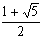
Retour en haut de page
On le désigne par la lettre grecque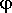 
( phi ) en hommage au sculpteur grec Phidias
(né vers 490 et mort vers 430 avant J.C) qui
décora le Parthénon à Athènes. C'est Théodore
Cook qui introduisit cette notation en 1914.
|
j
= |
|
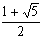Remarque
:
On
remarque que ce nombre est voisin du rapport
de deux nombres de Fibonacci consécutifs
(supérieurs à 3).
10 premiers termes
de la suite de Fibonacci
|
v1
= 1
v2 = 2
v3 = 1 + 2 = 3
v4 = 2 + 3 = 5
v5 = 3 + 5 = 8 |
v6
= 5 + 8 = 13
v7 = 8 + 13 = 21
v8 = 13 + 21 = 34
v9 = 21 + 34 = 55
v10 = 34 + 55 = 89
|
La suite de Fibonacci possède plusieurs particularités
intéressantes; nous en citerons deux.
| 1)
Si nous additionnons les n premiers termes
de la suite de Fibonacci, le nombre obtenu
est égal au terme de rang (n +2) moins
1, c'est-à-dire :
Pour ceux
qui connaissent le principe d'induction,
la preuve de ce résultat est aisée à
établir.
|
2) Si nous effectuons la division
d'un terme par celui qui le précède,
il nous semble que le quotient s'approche
de plus en plus de 1,6180......
qui est la valeur du nombre d'or.
En fait, lorsque n est de plus en
plus grand, le quotient du n ième
terme par celui qui le précède est
égal au nombre d'or. L'élève ayant
étudié un tant soit peu la notion
de limite peut démontrer que :
|
|
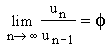
Retour en haut de
page
La dénomination
section d'or ou section dorée
est tardive et est due à l'Allemand Zeising,
au milieu du XIXème siècle (il dit "Der
goldene Schnitt").
La plus ancienne définition, et construction
géométrique, de la section d'or remonte au
IIIème siècle avant JC et est dûe au mathématicien
grec Euclide, dans son ouvrage Les Eléments
:
Le
partage en "extrême et moyenne raison"
d'un segment.
|
 |
Euclide |
D’après Euclide, un segment est partagé suivant
la section d'or ou la proportion divine si
les rapport x / y et y / (x - y)
sont égaux, ce qui signifie que le petit et
le moyen segment sont dans le même rapport
que le moyen et le grand segment.
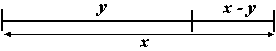
De l’équation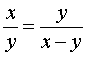 
,
on obtient l'équation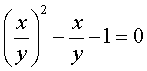 
dont la solution est :
|
 |
=
 |
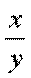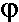Retour en haut de page
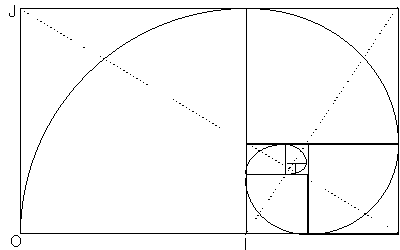
La figure est
construite à partir d'un grand rectangle d'or.
On retire le grand carré au grand rectangle
d'or et on obtient un petit rectangle d'or.
Ensuite, on retire le petit carré au petit
rectangle d'or et on obtient un rectangle
d'or plus petit.
On réitère l'opération indéfiniment. Elle
ne s'arrête pas car la longueur et la largeur
d'un rectangle d'or sont incommensurables
(on ne peut pas mesurer l'un en prenant l'autre
pour unité).
La spirale obtenue
est une spirale équiangulaire qui se rencontre
beaucoup dans la nature : tournesols, pommes
de pins, coquillages, disposition des feuilles
ou des pétales sur certaines plantes.
Les diagonales des rectangles se coupent au
même point C qui est le point limite de la
spirale.
Dans le repère (O, I, J), C(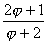 
; 
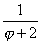) ou bien aussi C ( 
; 
).
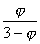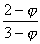La spirale est invariante par la similitude
de centre C, de rapport
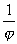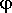( = - 1) et d'angle -p
/ 2.
Retour en haut de page
Le nombre d’or est utilisé en architecture,
en sculpture, en peinture, en sculpture, en
artisanat,...
Une forme d’un édifice, d’une statue, d’une
peinture, d’un instrument de musique est belle
lorsque les rapports entre ses diverses dimensions
respectent un certain nombre de lois géométriques
et perspectives : on parle de divine proportion.
Les Egyptiens avaient employé ce rapport en
lui donnant la valeur de 1,614. On le trouve
dans la pyramide de Kheops (le rapport de
l’apothème à la moitié d’un coté vaut 1,614)
et dans le temple de Louqsor, entre autres.
Les Grecs, qui s’en servirent pour le
Parthénon, attribuaient la découverte du
nombre d’or à Pythagore. C’est en 1226 que
Fibonacci énonça la valeur du nombre d’or :
1,618, et c’est à cette mesure que l’on
s’arrête habituellement. Le portail royal de
la cathédrale de Chartres en est un bel
exemple.
Ce nombre d’or est souvent la clé de
l’équilibre d’un tableau ou d’un construction.
Les peintres de la Renaissance, comme Titien
et Michel-Ange, s’en sont servis.
Certains théoriciens ont retrouvé le nombre
d’or dans le squelette humain, dans le sang
même, et ont déclaré que notre corps était
construit selon le nombre d’or.
Cas où le nombre
d'or intervient :
le Parthénon,
la pyramide de Chéops, le dôme de Milan,
de nombreuses peintures de la Renaissance
italienne(Léonard
de Vinci, Raphaël,...), les cathédrales
(Chartres,...), de nombreuses réalisations
de l’architecte
Le Corbusier (Modulor), les instruments
de musique(violons,...) les représentations
de dieux grecs (statues,..)...
Le nombre d’or est
aussi présent dans la nature :
|
Le
tournesol. On retrouve dans
la structure de cette plante le nombre
d’or ; en effet, les feuilles sont disposées
autour de la tige selon ce nombre.
|
Retour en haut de page
