Le
nombre d'or dans la musique
Les mathématiques
ont été beaucoup utilisés dans la musique, de
manière très diversifiée, car ils peuvent jouer des
rôle multiples. Plus précisément, nous avons recherché
de quel façon le nombre d'or a été utilisé
dans l'histoire musical,
et nous avons conclu que Bela Bartok était l'un des
compositeur l'ayant le plus introduit dans ses
oeuvres. Nous nous somme donc intéressé à ses oeuvres
de plus prés, afin de voir de quel façon il a mêlé la
"divine proportion" et la musique. C'est ce
que nous allons analyser ici.
-Un art qui allie beauté et équilibre-
L’étude
qui suit se propose de donner quelques
principes importants, nécessaires à la
compréhension des œuvres de Bartok.
Béla Bartok (1881-1945) :
Né
en 1881, après des études de piano et
d'harmonie à Bratislava puis à Budapest. Béla Bartók s’impose
de nos jours comme l’un des compositeurs
les plus importants du vingtième siècle. Il
s’est d’abord fait connaître comme pianiste et
ethnomusicologue. Avec son collègue et ami,
Zoltan Kodály, il a parcouru les campagnes
reculées d’Europe de l’Est, de 1907 à 1918,
pour recueillir des milliers de chants
folkloriques, un travail qui allait influencer
de façon décisive son inspiration de
compositeur. En particulier, Bartók a su
intégrer dans ses propres œuvres les
inflexions modales et les irrégularités
métriques qui caractérisaient un grand nombre
des chants traditionnels qu’il avait
répertoriés au cours de ses voyages.
La section d’or :
Un
élément capital dans la musique de Bartok est
la section d’or.
« La
musique est un exercice d’arithmétique
secrète, et celui qui s’y livre ignore qu’il
manie des nombres ». Cette remarque fut citée
par Leibnitz, mais il est très probable que
Bartok ne l’aurait pas refutée. En effet, très
épris de mathématiques,le compositeur était
fasciné par les structures régulières qu’on
peut trouver dans la nature, comme les
formations en spirale des coquilles d’escargot
ou l’ordre parfait des rangées d’un cône de
pin. Ces deux exemples d’architecture
naturelle illustrent l’une des plus anciennes
règles numériques qu’il a été convenu
d’appeler la règle d’or. Stipulée en termes
géométriques, la règle prescrit qu’une unité
soit divisible en deux parties de telle sorte
que le rapport de la plus grande partie à
l’unité soit le même que le rapport de la
petite partie à la plus grande. Les anciens
considérés qu’une forme, pour être « belle »
devait pouvoir être calculée selon le rapport
défini par la section d’or.
Bartok l’a souvent
utilisé pour la construction formelle de ses
œuvres.
En
termes numériques, on obtient un nombre
irrationnel de l’ordre de 0, 618… pour la
grande section et de 0, 382… pour la petite.
Il est frappant de constater que ces
proportions sont exactement celles qu’on
observe entre les cercles concentriques de la
coquille d’escargot et entre les rangées du
cône de pin. Bartók a utilisé à outrance ces
proportions pour déterminer les durées
relatives des différentes sections de ses
œuvres.
L’usage
d’un nombre irrationnel posant certaines
difficultés, une série arithmétique simple
permet de contourner le problème et de
s’approcher de la règle d’or avec une faible
marge d’erreur : les nombres de Fibonacci. On
obtient ceux-ci en additionnant à un nombre
son prédécesseur immédiat dans la série : 0 +
1 = 1, 1 + 1 = 2, 2 + 1 = 3, 3 + 2 = 5, etc.,
ce qui donne 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,
55, 89 et ainsi de suite. Plus on avance dans
la série, plus on s’approche de la règle d’or
en divisant n’importe quel nombre par son
successeur.
Musique pour
cordes, percussions et célesta 1936
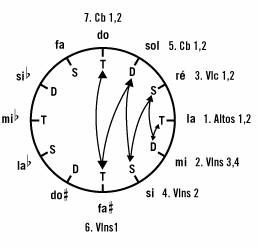Le
premier mouvement de la Musique pour cordes,
percussions et célesta est un des plus beaux
exemples de construction formelle suivant ce
procédé. Si l’on considère à nouveau les
premières mesures du mouvement, on remarque
que les entrées de la fugue correspondent aux
numéros de mesure suivants:
Altos 1, 2 : mesure
1
Violons 3, 4 : mesure
5
Violoncelles 1, 2 : mesure
8
Violons 2 : mesure
13
Contrebasses : mesure
18
Violons 1 : mesure
27
Les
quatre premières entrées correspondent aux
nombres de Fibonacci. Il manque les nombres 2,
3 et 21. Aux mesures 2 et 3, les altos
énoncent les deuxième et troisième phrases du
thème, bien délimitées par un demi-soupir. La
mesure 21 marque la fin de l’énonciation du
thème aux contrebasses et entame un court
épisode avant l’entrée des premiers violons à
la mesure 27. On se rappellera qu’à cet
endroit commence une transition qui mène à
l’entrée de la timbale à la mesure 34, un
autre nombre de Fibonacci…
Comment
alors expliquer les entrées aux mesures 18 et
27 ? Il faut ici considérer des raisons
d’ordre purement pratique. Il va de soi que
plus on avance dans la série de Fibonacci,
plus il faudra laisser du temps à la musique
avant d’atteindre le nombre de mesure désiré
pour pouvoir enfin y établir un moment formel
important. Bartók se devait donc de trouver un
moyen d’insérer ses moments musicaux
d’importance secondaire entre les grandes
frontières formelles. Il a donc décidé de
faire des subdivisions à l’intérieur des
grandes sections délimitées par les nombres de
Fibonacci. Ainsi, de la mesure 13 (entrées des
seconds violons) à la mesure 21 (début de
l’épisode), on compte huit mesures. Si l’on
divise ce groupe de huit mesures en deux
sous-groupes de cinq et trois mesures (rapport
de Fibonacci de 5 : 3), on obtient l’entrée
des contrebasses à la mesure 18. De même, si
l’on considère le passage de la mesure 13 à la
mesure 34, on compte vingt et une mesures,
qui, une fois subdivisées à leur tour en deux
autres sous-groupes de quatorze et sept
mesures (rapport de Fibonacci de 2 : 1) nous
donnent l’entrée des premiers violons à la
mesure 27.
Conclusion :
La
musique de Béla Bartok est un art qui allie
beauté et équilibre. En plus de cette étude
sur les entrés des différents instruments, il
faut savoir que les structures de sons, par
exemple, répondent elles aussi aux
préoccupations du compositeur vis-à-vis de la
nature. En ce sens, les intervalles mélodiques
et harmoniques de la Musique pour cordes,
percussion et célesta sont eux-mêmes choisis à
partir des nombres de Fibonacci. Ces quelques
exemples démontre le souci du compositeur pour
concevoir chaque œuvre comme un ensemble
harmonieux qui soit régi par une seule loi
universelle. Ce souci d’équilibre en fait un
compositeur bien de son temps, à une époque où
la science cherchait désespérément à expliquer
l’univers en un principe « unique, simple et
beau », pour citer Einstein. Les scientifiques
n’y sont pas encore parvenus, mais Bartók, par
sa musique, a pu au moins nous en donner une
illustration saisissante.
Retour en haut de
page
